Monty Hall Problem Simulator

Le problème de Monty Hall est l’un des problèmes mathématiques les plus connus dans le domaine de la théorie des probabilités:

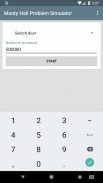
Dans un jeu télévisé, l'hôte demande à un joueur de choisir une des trois portes fermées devant le joueur. Derrière deux portes se trouvent des chèvres et derrière une porte, une voiture que le joueur peut gagner quand il choisit cette porte. Une fois que le joueur a sélectionné une porte (qui reste fermée), l’hôte ouvre une autre porte sur laquelle se trouve une chèvre. L'hôte demande alors au joueur s'il veut rester à la porte qu'il a choisie au début ou s'il veut passer à l'autre porte fermée.

La question est évidemment la suivante: le joueur doit-il changer de porte ou rester à la porte sélectionnée?

Beaucoup de gens pourraient dire que peu importe que le joueur change de porte ou non, car la probabilité de gagner la voiture est de 50/50. Même si cela semble raisonnable car il y a deux portes closes identiques, c'est la mauvaise réponse.

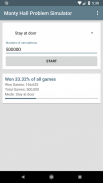
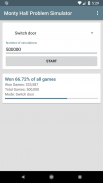
La bonne réponse est que la chance de gagner la voiture est de 67% lorsque le joueur change de porte et de seulement 33% lorsque le joueur reste à la porte qu’il a choisie en premier.

Ne crois pas encore rencontré? Il suffit de télécharger l'application et l'essayer!

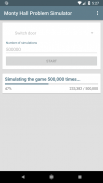
Cette application vous permet de simuler automatiquement le scénario de jeu décrit jusqu'à 5 millions de fois de suite. Vous pouvez choisir si vous voulez que le joueur simulé passe toujours la porte ou reste toujours à la porte qu’il a sélectionnée en premier. Une fois que l'application a simulé le nombre de jeux requis, vous obtenez une statistique indiquant le nombre de parties gagnées par le joueur. De cette façon, vous pouvez savoir si le joueur doit ou non changer de porte.